4.4Radio de convergencia

En matemáticas, según el teorema de Cauchy-Hadamard, el radio de convergencia de una serie de la forma , con , viene dado por la expresión:

 Definición

 Si nos limitamos al conjunto de los números reales, una serie de la forma , con , recibe el nombre de serie de potencias centrada en x₀. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x₀ | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x₀ − r, x₀ + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x₀, r = 0. Si lo hace para cualquier valor de x, r =.

Ejemplos

Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.

Radio de convergencia finito

La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potenciax − x₀ = x − 0 = x, tiene el siguiente aspecto:

.

(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x₀ = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho

.

(la cuenta se puede hacer por serie de potencia). Y por otro lado

.

Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x= 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:

.

Distancia a la singularidad

El cálculo del radio de convergencia no es simple. Veamos una función con dos desarrollos en serie con distintos centros y analicemos sus radios de convergencia. La misma función 1 / (1 − x) en su desarrollo con centro x₀ = 3tiene la forma:

.

Pero en este caso su radio de convergencia es r = 2. Notemos que la función 1 / (1 − x) tiene una singularidad en el 1; y que en los dos caso anteriores el radio de convergencia coincide con la distancia del centro a la singularidad: | 0 − 1 | = 1 y | 3 − 1 | = 2. Esto será siempre verdadero para ésta función, pero, no puede generalizarse, como veremos en el siguiente ejemplo:

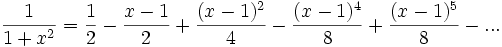
Como no hay singularidades reales podría suponerse que el radio es infinito, sin embargo su radio de convergencia es . Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie

Radio de convergencia infinito

Por ejempo, la función e^x puede desarrollarse en series de potencia de x − 0 =x, de hecho .

y esto vale para todo real x por eso el radio de convergencia será infinito

4.6 Representacion de Funciones mediante la Serie de Taylor

4.7 Calculo de Integrales Expresadas Como Serie deTaylor

Teorema de Taylor

En cálculo, el teorema de Taylor, recibe su nombre del matemático británico Brook Taylor, quien lo enunció con mayor generalidad en 1712, aunque previamente James Gregory lo había descubierto en 1671. Este teorema permite obtener aproximaciones polinómicas de una función en un entorno de cierto punto en que la función sea diferenciable. Además el teorema permite acotar el error obtenido mediante dicha estimación

Caso de una variable

Este teorema permite aproximar una función derivable en el entorno reducido alrededor de un punto a: E (a, d) mediante unpolinomio cuyos coeficientes dependen de las derivadas de la función en ese punto. Más formalmente, si   ≥ 0 es un entero y   una función que es derivable   veces en el intervalo cerrado [ ,  ] y  +1 veces en el intervalo abierto ( ,  ), entonces se cumple que:¹

(1a)

O en forma compacta

(1b)

Donde   denota el factorial de  , y   es el resto, término que depende de   y es pequeño si   está próximo al punto  . Existen dos expresiones para   que se mencionan a continuación:

(2a)

donde   y  , pertenecen a los números reales,   a los enteros y   es un número real entre   y  :²

(2b)

Si   es expresado de la primera forma, se lo denomina Término complementario de Lagrange, dado que el Teorema de Taylor se expone como una generalización del Teorema del valor medio o Teorema de Lagrange, mientras que la segunda expresión de R muestra al teorema como una generalización del Teorema fundamental del cálculo integral.

Para algunas funciones  , se puede probar que el resto,  , se aproxima a cero cuando   se acerca al ∞; dichas funciones pueden ser expresadas como series de Taylor en un entorno reducido alrededor de un punto   y son denominadas funciones analíticas.

El teorema de Taylor con   expresado de la segunda forma es también válido si la función   tiene números complejos o valores vectoriales. Además existe una variación del teorema de Taylor para funciones con múltiples variables.

[editar]Caso de varias variables

El teorema de Taylor anterior (1) puede generalizarse al caso de varias variables como se explica a continuación. Sea B una bola en R^N centrada en el punto a, y f una función real definida sobre la clausura   cuyas derivadas parciales de orden n+1 son todas continuas en cada punto de la bola. El teorema de Taylor establece que para cualquier  :

Donde la suma se extiende sobre los multi-índices α (esta fórmula usa la notación multi-índice). El resto satisface la desigualdad:

para todo α con |α|=n+1. Tal como sucede en el caso de una variable, el resto puede expresarse explícitamente en términos de derivadas superiores (véase la demostración para los detalles).

[editar]Demostración

Para demostrar el teorema de Taylor para el caso multidimensional, considérese un función   o campo escalar, que suponemos continuo y, para simplificar lo expuesto (aunque una generalización es trivial), de clase  . Sear(t) una función vectorial que va de  , y definamosla cómo  (de ahora en adelante,vse omitirán las flechas de los vectores).Pongamos r(t) = y Ahora hagamos g(t) = f[r(t)] y recordemos que  . Notemos ahora que:

Ahora, derivando sucesivas veces, encontramos que podemos poner de forma muy cómoda:

donde el exponente sobre el gradiente es entendido cómo las sucesivas veces que hacemos el gradiente; es decir,hacemos el producto escalar que está dentro del paréntesis,luego volvemos a derivar otra vez la función, obteniendo otro producto escalar, y así "n" veces. Ahora, empleando el teorema de Taylor para una variable real, expandimos g(t) en su serie de McLaurin:   y haciendo t=1 y sustituyendo las derivadas por las expresiones antes hallada se evidencia que:   Obsérvese que el primer término aparece el gradiente y en el segundo la matriz hessiana, pero escrito con esta notación particular que resulta más cómodo y compacto. La expresión obtenida es equivalente a la expresada más arriba mediante la notación multiíndice.

[editar]Demostración

La demostración de la fórmula (1a), con el resto de la forma (2a), se sigue trivialmente del teorema de Rolle aplicado a la función:

Un cálculo rutinario permite ver la derivada de esta función cumple que:

Se define ahora la función G como:

Es evidente que esta función cumple  , y al ser esta función diferenciable, por el teorema de Rolle se sigue que:

Y como:

Se obtiene finalmente que:

Y substituyendo en esta fórmula la definición de F(a), queda precisamente la fórmula (1a) con la forma del resto (2a).